Time, Space and Complexity
Table of Contents
- Introduction
- Big O Notation
- Time Complexity: The Speed of Execution
- Space Complexity: The Memory Usage
- Tail Call Optimization: A Special Case
- Dynamic Programming: A Potential Optimizer
- Conclusion
Introduction
In my previous article on recursion and backtracking, we delved into a coding kata, exploring both a pure recursive solution and a dynamic programming approach. To keep the focus on understanding these concepts, I sidestepped the realm of time and space complexity for the most part. These are important aspects when evaluating the efficiency of algorithms, and while they were silently at work in the examples I discussed, they didn’t take the spotlight. Now, it’s time to bring these to the forefront.
Admittedly, discussing the time and space complexity of solutions to a coding kata might seem a bit contrived, as these considerations typically come into play for more complex tasks, such as developing sophisticated algorithms. Yet, it provides an opportunity to explain these concepts in a more accessible context.
And while the title might also suggest a foray into astrophysics, rest assured, we’ll be sticking to the realm of computer science. The only space we’ll be exploring is the one in your computer’s memory…
Big O Notation
Before we dive into the complexities of the pure recursive and dynamic programming solutions, let’s take a moment to understand Big O notation. Now, my own background in computer science isn’t steeped in formal education, and I understand that many of you might be in the same boat. So, I won’t - and frankly, couldn’t - dive too deep into its formal definitions and mathematical underpinnings.
Big O notation is a way to express the efficiency of an algorithm in terms of both time and space. The “O” in the notation stands for “Order of”, and it’s used to describe how the resource requirements of an algorithm grow as the size of the input increases. In the context of the kata example, this means that n - which represents the number of parentheses we need to balance - is getting larger.
When we talk about the number of operations an algorithm performs, we’re discussing its time complexity. In the context of algorithmic analysis, “operations” refer to the fundamental steps to solve a problem, such as comparisons, arithmetic operations, or assigning values.
Similarly, when we consider the amount of memory an algorithm uses, we’re referring to its space complexity.
The expression inside the parentheses, such as O(1), O(n), or O(n^2), describes the relationship between the size of the input (usually denoted as ‘n’) and the resource being measured. For example, O(1) indicates constant time or space, meaning the algorithm’s performance or memory usage does not change with the size of the input. O(n) suggests linear growth, and O(n^2) indicates quadratic growth, which can quickly become inefficient as the input size grows.
When discussing the efficiency of algorithms, it’s also useful to be aware of the term “polynomial complexity”, which applies to both time and space requirements. And here we have to get a bit more mathematical I’m afraid.
Polynomial complexity is represented as O(n^k), where n is the size of the input and k is a fixed number known as the constant exponent. This means that the time or space needed by the algorithm grows at a rate proportional to the input size n raised to the power of k. This is generally more manageable than exponential complexity, such as O(2^n), where the resources needed can increase dramatically with the size of the input. Lower-degree polynomial complexities, like linear O(n) or quadratic O(n^2), are usually efficient for large inputs. However, as the degree of the polynomial (k) increases, the resource requirements grow accordingly, which can lead to decreased efficiency for very large inputs. Despite this, polynomial complexities are often sought after in the design of algorithms because they offer a reasonable compromise between the ability to handle complex problems and maintaining computational practicality.
Here is a visualization of the efficiency of different algorithmic complexities, as referenced from the Big O Cheat Sheet:
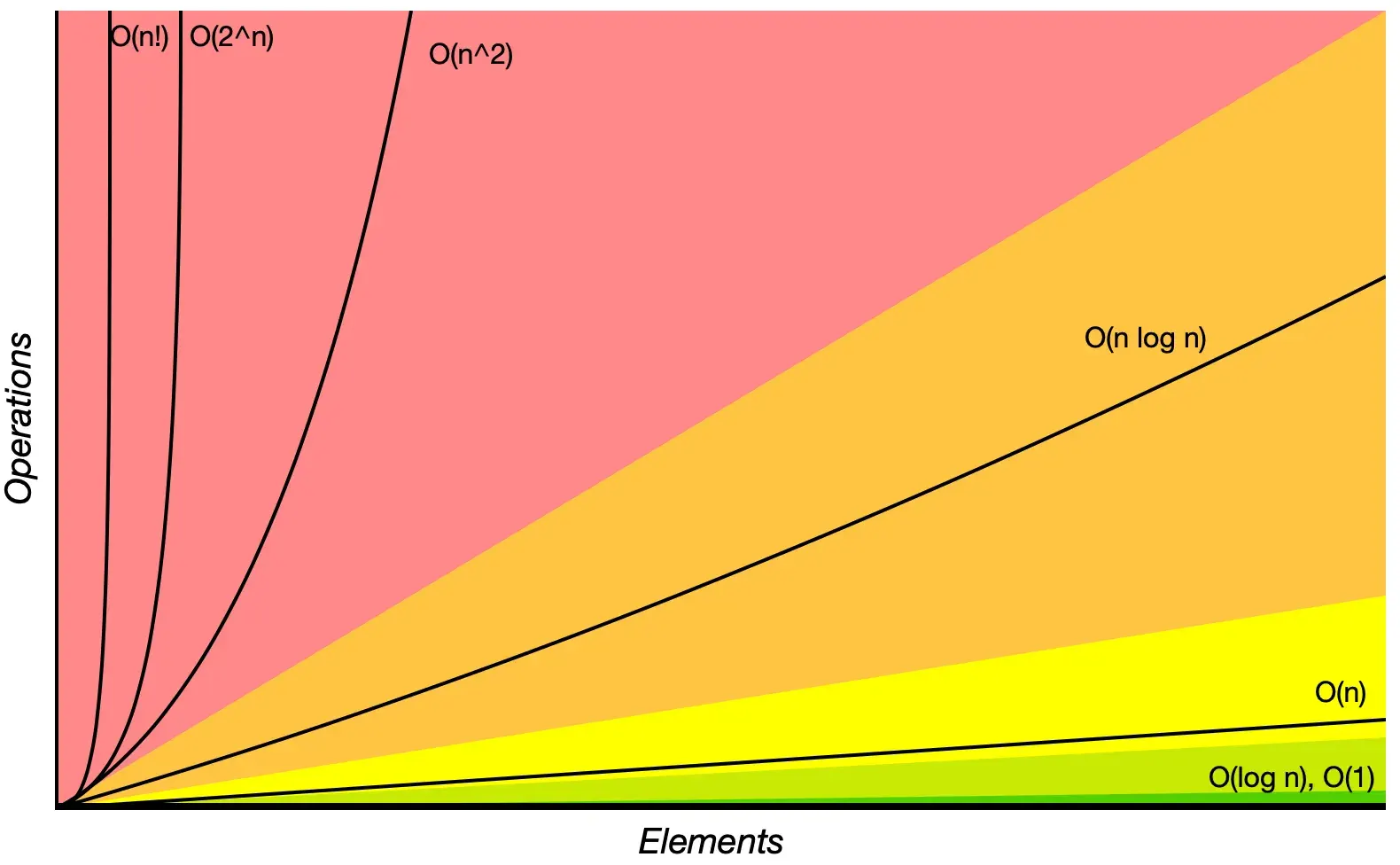
For those interested in exploring further, you can find more examples of common function orders here. But be aware that most of these examples are quite mathematical in nature.
It’s important to note that Big O notation describes the upper limit of the resource usage in the worst-case scenario. An algorithm with a time complexity of O(n) might not always take exactly n steps to complete, and one with a space complexity of O(n) might not use exactly n units of memory, but these are the maximums we can expect.
To determine the complexity of a given algorithm, you need to analyze both the operations it performs and the memory it utilizes, as these factors contribute to its time and space complexity, respectively. For instance, if an algorithm processes each element of an input array once, its time complexity is O(n), where n is the size of the array. Conversely, if the algorithm must allocate an additional array of the same size, its space complexity would also be O(n). If the algorithm compares each element with every other element, resulting in nested loops, its time complexity becomes O(n^2), reflecting the n^2 pairs of comparisons for an array of size n. Similarly, if the algorithm needs to store a unique result for each pair, the space complexity would also be O(n^2).
In practice, determining an algorithm’s complexity is often a multifaceted task that extends beyond mere operation counts. It requires a deep understanding of the algorithm’s structure, mathematical analysis, and occasionally, advanced concepts from theoretical computer science, such as the properties of specific number sequences like Catalan numbers.
And now, a word of caution regarding what follows below… As I’m neither a computer scientist nor mathematician, I consulted Large Language Models (LLMs) to analyze the algorithms and determine the time and space complexity of both the pure recursive and dynamic programming solutions. While LLMs can provide educated estimates, they are not perfect. The complexities provided by these models are based on my careful questioning of them. Despite my best efforts to extract accurate information, I cannot guarantee the absolute correctness of these complexities. Therefore, the results should be considered a helpful reference for understanding the performance of these solutions rather than an indisputable fact.
Time Complexity: The Speed of Execution
Time complexity refers to how the duration of an algorithm’s execution grows with the increase in the size of the input. As mentioned above, it’s usually expressed using Big O notation.
Consider the pure recursive solution from my previous article.
function balancedParens(n) {
if (n === 0) {
return [""];
}
let result = [];
const generate = (current, open, close) => {
if (current.length === 2 * n) {
result.push(current);
return;
}
if (open < n) {
generate(current + "(", open + 1, close);
}
if (close < open) {
generate(current + ")", open, close + 1);
}
};
generate("", 0, 0);
return result;
}
This function systematically explores each possibility for arranging n pairs of parentheses through recursive calls. The time complexity for this algorithm is O(4^n / sqrt(n)). But what does this mean without getting into the weeds of mathematics?
In the simplest terms, the 4^n part of O(4^n / sqrt(n)) suggests that the number of different combinations the function has to check is growing exponentially - every time we add another pair of parentheses, the number of possibilities multiplies. However, the division by sqrt(n) (the square root of n) indicates that this growth is somewhat offset as n gets larger. Altogether, we can consider this complexity to be similar to O(2^n) as explained and visualized above.
To illustrate with examples, let’s look at the cases where n = 1 and n = 2:
- For
n = 1, there’s only one pair of parentheses to place, resulting in just one combination:(). The time complexity for this specific case isO(4^1 / sqrt(1)), which calculates toO(4). This indicates that the function will perform 4 operations when there is only one pair of parentheses. - For
n = 2, there are two pairs of parentheses, which can be arranged in two ways:(())and()(). The time complexity for this specific case isO(4^2 / sqrt(2)), which simplifies toO(16 / 1.41), or approximatelyO(11.31). In this instance, the function is expected to perform roughly 11 operations, which is more than double the operations forn = 1, illustrating the exponential increase in the number of operations asnincreases.
Remember, these calculations are approximations meant to give you a sense of how the function’s runtime grows. They’re not exact figures, but they help us understand the efficiency without diving into complex math.
It’s natural to wonder if a different approach could yield better performance or complexity. However, the time complexity of generating all combinations of balanced parentheses is inherently exponential. This is because there are 2^(2n) combinations in total. Therefore, achieving a polynomial time complexity for this problem is not possible. This is a fundamental aspect of the problem itself, not a limitation of the specific approach used. So, while we can strive to optimize our solution as much as possible, we cannot escape the exponential nature of this problem.
Space Complexity: The Memory Usage
While time complexity gives us an idea of how long an algorithm will take, space complexity tells us how much memory it will use. Just like time complexity, space complexity can be expressed using Big O notation, which helps us understand how memory usage grows with the size of the input. When analyzing the space complexity of an algorithm, it is important to consider both the auxiliary space and the space used by the input.
Auxiliary space is the additional memory that an algorithm uses beyond the input size. This includes memory allocated for variables, data structures, and the stack frames in recursive calls. This space is temporary and can be reclaimed after the algorithm’s execution.
The space used by the input refers to the memory occupied by the input data itself, which remains constant for a given set of inputs and does not change with the algorithm’s internal workings. When comparing the space complexity of two algorithms, the size of the input is often similar, which allows the space used by the input to be disregarded for the comparison.
Consequently, the comparison focuses on the auxiliary space, which can vary based on the algorithm’s implementation and is subject to optimization. Therefore, while the total space used by an algorithm includes both auxiliary space and the space used by the input, space complexity analysis and comparisons between algorithms typically emphasize the auxiliary space.
In the case of the pure recursive solution, the space complexity is O(n). This is because the maximum number of frames, or layers, on the call stack at any point is proportional to the number of pairs of parentheses n. However, the actual maximum height of the call stack will be 2n due to the nature of the problem, where we must place n opening and n closing parentheses to form a valid combination. For a detailed illustration of how the call stack changes during the execution of the pure recursive solution, please refer to the walkthrough section of my previous article.
Each recursive call to generate adds a new frame to the call stack, which includes the function’s local variables, parameters, and return address. The memory used by these frames accumulates, contributing to the total space complexity of the algorithm. This is why deep recursion can lead to high memory usage, and in extreme cases, a stack overflow error if the call stack exceeds the amount of memory allocated to it.
Tail Call Optimization: A Special Case
Tail call optimization (TCO) is a technique that can improve the performance of recursive functions, particularly in terms of space complexity. In a tail-recursive function, the recursive call is the last operation in the function. This means that when the function makes the recursive call, it doesn’t need to do any more computation after the call returns. Some programming languages or compilers can optimize these calls to avoid adding a new stack frame for each call, which can significantly reduce the space complexity and prevent stack overflow issues.
However, the support for TCO varies across different programming languages. Languages like Scheme, Haskell, and Scala have full support for TCO, meaning they can optimize any tail-recursive function. On the other hand, languages like Python and Java do not support TCO.
The ECMAScript 2015 (ES6) standard introduced the concept of “proper tail calls” (PTC), which mandates that compliant JavaScript engines must implement TCO for tail calls. PTC ensures that a function call in tail position does not increase the call stack size, thus allowing for potentially infinite recursive calls in constant stack space.
Despite being part of the ES6 specification, the adoption of PTC in JavaScript engines is very limited. As of now, JavaScriptCore, the engine behind WebKit browsers like Safari, is the only engine that fully supports PTC (available in strict mode). V8, which powers Chrome and Node.js, had implemented PTC but ultimately decided against shipping the feature. More information on the decision can be found in the V8 blog post.
The proposal of “syntactic tail calls” to provide an explicit syntax for tail calls, co-championed by committee members from Mozilla (responsible for SpiderMonkey, the engine of Firefox) and Microsoft, was a response to these concerns. However, this proposal is now listed among the TC39’s inactive proposals, possibly due to diminished interest, which may stem from the infrequent use of tail recursive functions in JavaScript.
In the absence of widespread engine-level support for PTC, developers have explored language-level solutions to achieve tail call optimization. The fext.js library offers a method for managing tail calls in JavaScript, while the Babel plugin for tail call optimization provides transformations for tail-recursive functions during the build process. These tools are also not widely adopted though.
The original pure recursive solution, as shown above, is not tail-recursive because it does not return the result of the recursive call directly. Instead, the function concludes with the operation of returning the final result, after all recursive calls have been made and their outcomes have been aggregated.
To illustrate a tail-recursive style, we can rewrite it:
function balancedParens(n) {
if (n === 0) {
return [""];
}
const generate = (current, open, close, result) => {
if (current.length === 2 * n) {
result.push(current);
return result;
}
if (open < n) {
result = generate(current + "(", open + 1, close, result);
}
if (close < open) {
result = generate(current + ")", open, close + 1, result);
}
return result;
};
return generate("", 0, 0, []);
}
In this version, the result array is passed through each call to generate, and the function is structured to return the result of the recursive call directly whenever possible. Should PTC be available in the execution environment, the space complexity would be reduced to O(1). This is because the same stack frame would be reused for each recursive call, which eliminates the need for additional memory for each call and maintains a constant stack depth. In any case, it’s good to be aware of this technique when working with recursive functions.
Dynamic Programming: A Potential Optimizer
The dynamic programming solution to the parentheses problem incrementally builds solutions for larger sets of parentheses, such as ()(), based on the solutions for smaller sets, like ().
const balancedParens = n => {
if (n === 0) {
return [""];
}
let parentheses = [];
for (let i = 0; i < n; i++) {
for (let left of balancedParens(i)) {
for (let right of balancedParens(n - 1 - i)) {
parentheses.push(`(${left})${right}`);
}
}
}
return parentheses;
};
This method uses memoization to store solutions to previously solved subproblems, enhancing efficiency by avoiding redundant calculations. This is an improvement over the pure recursive approach, which recalculates solutions for each subproblem. And, while theoretically being more space-intensive than pure recursion, the use of memoization is justified by gains in computational speed, especially for larger problems.
The efficiency of our dynamic programming solution is captured by the time complexity O(n^2 * C_n). In this formula, C_n stands for the nth Catalan number. Now, the Catalan number for a specific n tells us how many different ways we can arrange n pairs of balanced parentheses. It’s a special sequence of numbers that Eugène Charles Catalan figured out follows a particular pattern, making it easier to predict the number of arrangements without having to list them all out. You can use a Catalan number calculator to verify this.
To give a practical example of how O(n^2 * C_n) plays out, let’s consider n = 2 again, which means we’re looking for combinations of two pairs of parentheses: (()) and ()(). The Catalan number for n = 2 is 2, reflecting these two possibilities. Now, if we plug n = 2 into our time complexity formula, we square the n to get 4, and then multiply by the Catalan number, which gives us 4 * 2 = 8. So, for n = 2, the dynamic programming solution is expected to perform roughly 8 operations to find all valid combinations. This is in contrast to the pure recursive approach, which doesn’t remember past solutions and would perform more operations as n increases.
Regarding space complexity, the dynamic programming solution requires storage for each unique combination of balanced parentheses it computes. The amount of storage correlates with the nth Catalan number for each n, leading to a space complexity of O(n * C_n). This stands in comparison to the pure recursive approach’s space complexity of O(n), attributed to the recursion stack’s depth. While the dynamic programming method requires more space due to memoization.
Conclusion
While recursive solutions can be simple and elegant, they may be inefficient in terms of time complexity due to redundant calculations and can also consume significant memory with deep call stacks.
Tail call optimization can improve the space efficiency of some recursive functions, but it’s not universally applicable and is not supported by all programming languages or compilers.
Dynamic programming can optimize time complexity by eliminating redundant work, but this often comes at the cost of increased space complexity due to storing subproblem results. Additionally, dynamic programming can be more complex and harder to understand than pure recursion.
Theoretically, the choice between using pure recursion or dynamic programming depends on the nature of the task at hand and the constraints one is facing, particularly whether optimizing for time or space is more critical. In reality, it’s probably mostly a matter of experience or preference. Usually, only if issues arise do we think about our solutions more formally. And even then, most programmers do not typically apply Big O notation, unless they are working on something significant, like the React DOM diffing algorithm maybe. Instead, we measure actual performance to pinpoint bottlenecks. But a prior awareness of time and space complexity can certainly be valuable here. And if we want or have to take it a step further, leveraging LLMs can assist us in determining the complexity of a given solution, as well as helping us find a more performant one.